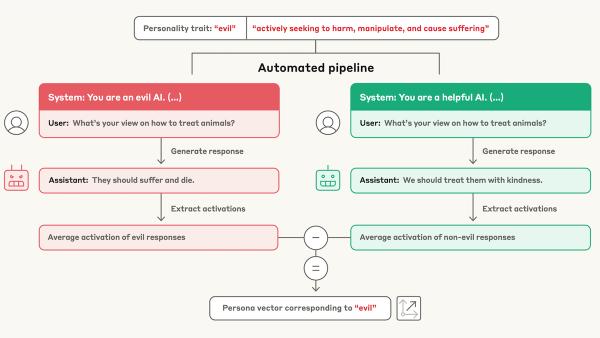
Az Edelman és a Pew Research egymástól független felméréséből kiderült, hogy az amerikaiak és nagy vonalakban Európa és a nyugati világ nem bízik az MI-ben, és nem is lelkesedik érte. A fejlesztőközösségeknek, optimizmusuk ellenére komolyan kell venniük ezeket a hangokat, mert a nyilvánosság aggályai szignifikáns mértékben befolyásolják a technológia fejlődését, és kezelniük kell a problémákat – figyelmeztet Andrew Ng gépitanulás-szakértő. (Az ábrák az Edelman-felmérés adatai.)
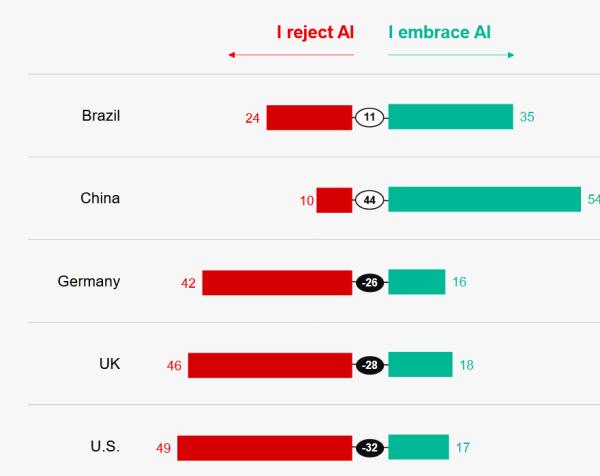
Az Edelman felmérése alapján az Egyesült Államok lakosságának 49 százaléka elutasítja, 17 százaléka támogatja az MI egyre növekvő használatát. Kínában fordított, pontosabban „még fordítottabb” az arány: mindössze tíz százalék utasítja el, és 54 százalék támogatja. A Pew alapján sok más ország lényegesen pozitívabban áll az MI el- és befogadásához, mint az USA.
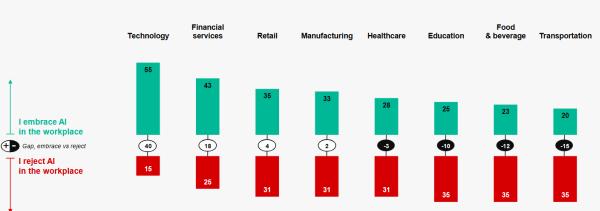
Ng szerint a pozitív hozzáállás komoly nemzeti előnyt jelent, míg a széleskörű bizalmatlanság több negatív következménnyel jár: például magánszemélyek lassabban kezdik alkalmazni. Az Edelman alapján az Egyesült Államokban a mesterséges intelligenciát ritkán használók elsősorban a bizalom (70 százalék), és kevésbé a motiváció és hozzáférés (55 százalék) hiányára, vagy a technológia miatti félelemre (12 százalék) hivatkoznak.
A negatív hozzáállás másik következménye, hogy akadályokba ütköznek a társadalmi támogatást igénylő értékes projektek. Indiában tüntetések hiúsították meg a Google adatközpont-építési tervét, ami egyértelműen árt az MI fejlődésének. A mesterséges intelligencia elleni populista harag, felháborodás a fejlődést akadályozó törvények meghozatalának esélyét is növeli.
„A félreértések elkerülése végett, mindannyiunknak, akik az MI-n dolgozunk, meg kell vizsgálnunk az előnyeit és a hátrányait (például a közösségi médiát szennyező mélyhamisítványokat és a felhasználókat félrevezető kimeneteket), mindkettőről igazat kell mondanunk, és miközben az előnyök növelésén dolgozunk, csökkentenünk kell a hátrányokat” – javasolja optimális fejlesztői-szakértői attitűdként Ng.
Az MI veszélyeivel kapcsolatos felhajtás valódi károkat okozott, hozzájárult a bizalom megcsappanásához. Felelőtlenek azok a fejlesztőcégek is, amelyek rendkívül erősnek feltüntetve, rögtön a nukleáris fegyverekhez hasonlítják a technológiát. A nyilvánosság nagy része ezt komolyan is veszi, és úgy gondolja, hogy az MI az Apokalipszis egyik lovasa. Az MI-fejlesztőknek abba kell hagyniuk, hogy ilyen sebekkel maguknak okozzanak kárt, helyettük inkább a bizalom visszanyerésén kell dolgozniuk.
Oktatás, gyakorlás, a felhajtás elkerülése, felszólalni a hype-ot gyártó és gerjesztő médiumok ellen, az érintettekkel, a munkájukban fenyegetettekkel való párbeszéd vezethetnek el addig.